妥当性の主張文例

妥当性の主張ー支配方程式

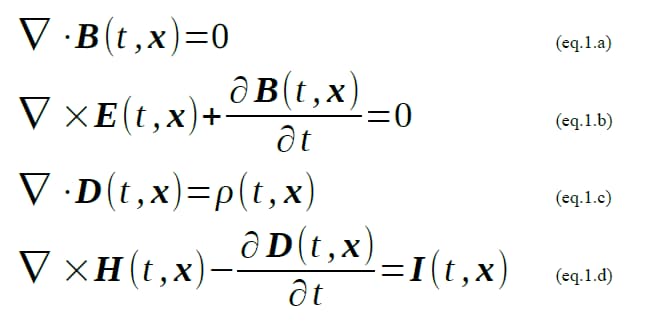
文例: conventional-FDTDの場合

支配方程式を(eq.1.b), (eq.1.d)としD = ε0E、H = 1/μ0Bの関係を用いて電界E及び磁界Hの方程式に書き換えた2式を以下の手法で解いた。

文例: RC-FDTDの場合

支配方程式を(eq.1.b), (eq.1.d)とし電束密度Dを電界の畳み込み積分を帰納的に求めるRC ( Recursive Convolution )法を用いて電界Eで表現し、磁束密度BをH = 1/μ0Bの関係を用いてHで書き換えた2式を以下の手法で解いた。

文例: RC-FDTDの場合（英文）

RC-FDTD (Recursive Convolution – Finite Difference Time Domain method) is applied in simulations. The governing equations of RC-FDTD are (eq.2) and (eq.3).

(eq.2) is rewritten into time difference form (eq.4) considering B=μH. In RC-FDTD to consider dispersive properties electric flux density D is obtained by recursive convolution. When ε’(ω)-ε’’ (ω)=ε∞+Χ(ω), current density J=0 and electric conductivity σ=0 are assumed (eq.3) is rewritten as time difference form (eq.5).

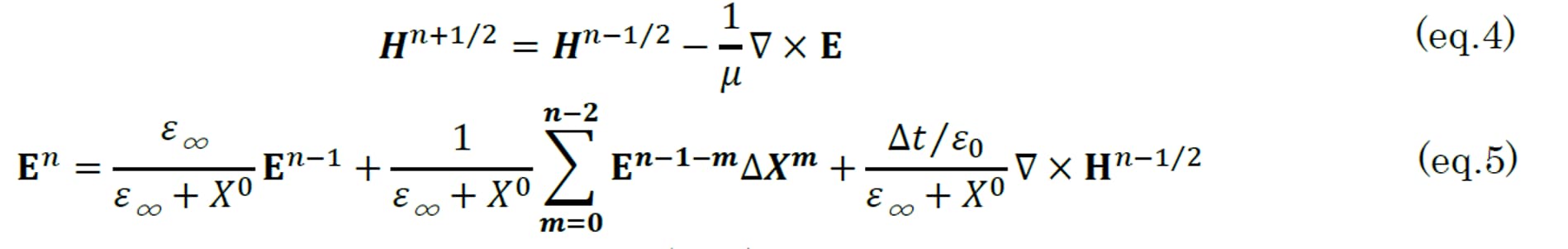
Because constant permeability is assumed (eq.4) is same as conventional FDTD method. Here the summation of 2nd term of right hand side of (eq.5) is replaced by recursive accumulator Φn-1 and (eq.5) rewritten by (eq.6).

Χ0 = X10+ X20+ X30 and Φn-1 are calculated from linear summation of recursive accumulators corresponding to each dispersion model. The reference describes details.

まとめ

商用のソフトウェアを用いてシミュレーションを行って報告書や論文に纏める際に「ソフトウェア名と使用モジュール名を記載して終わり」という文書を散見します。これはソフトウェアを所有しない人にとっては無用の長物ですし、「再現性の確保」という点で不十分です。少なくとも支配方程式は記載するべきです。

Maxwell方程式は巨視的な電界E及び電束密度D、磁界H、磁束密度Bの空間と時間における関係を示しています。FDTD法による電磁波解析の支配方程式は上記4式のうち、Faraday-Maxwellの式(eq.1.b)とAmpere-Maxwellの式(eq.1.d)です。

この2式で4つの物理量、電界E及び電束密度D、磁界H、磁束密度Bを求めているわけではなくconventional-FDTD法ではD = ε0E、H = 1/μ0Bの関係を用いて電界E及び磁界Hの方程式に書き換えて2式で方程式を閉じています。物性の分散性を扱う場合はこの単純な関係を用いることが出来ないので後述するRC-FDTD法を用いますが、この場合も電界Eと磁界Hの方程式を解いていることは共通です。

シミュレーション対象の現象を物理的に記述する支配方程式の記載は論文・報告書などでは必須です。

妥当性の主張ー物性値または物性モデル

文例: 固定物性の場合

物性値の決定に関して、系の温度20℃、励振源の周波数2.45GHzを想定した。キャビティの金属は完全導体を仮定した。容器のパイレックス製ビーカーはメーカー提供のカタログに記載された複素誘電率ε’-jε”=4.6 – j0.023を与えた。水は複素誘電率ε’-jε”= 79.1 – j7.8とした。

文例: 分散性を考慮した場合

周波数2.45GHz、温度20℃に対応する電解液の複素誘電率は Debye モデルと Drude モデル（eq.1）でモデル化した。

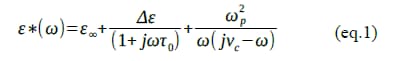
分散パラメータは ε∞ =12.4 、 ∆ε = 72.8 、 τ0=1.36×10-11 [sec] 、 ωp = 1.46×1011 [rad/sec] 、 νc = 3.64×1010[rad/sec]とした。

文例: 分散パラメータをtable表示した例（英文）

Dielectric constant for water and Intracellular Water ( IW ) are modeled by tri-pole function (eq.1). This function includes a pole derived from slow Debye relaxation, one from fast Debye relaxation and one from Lorentz relaxation.

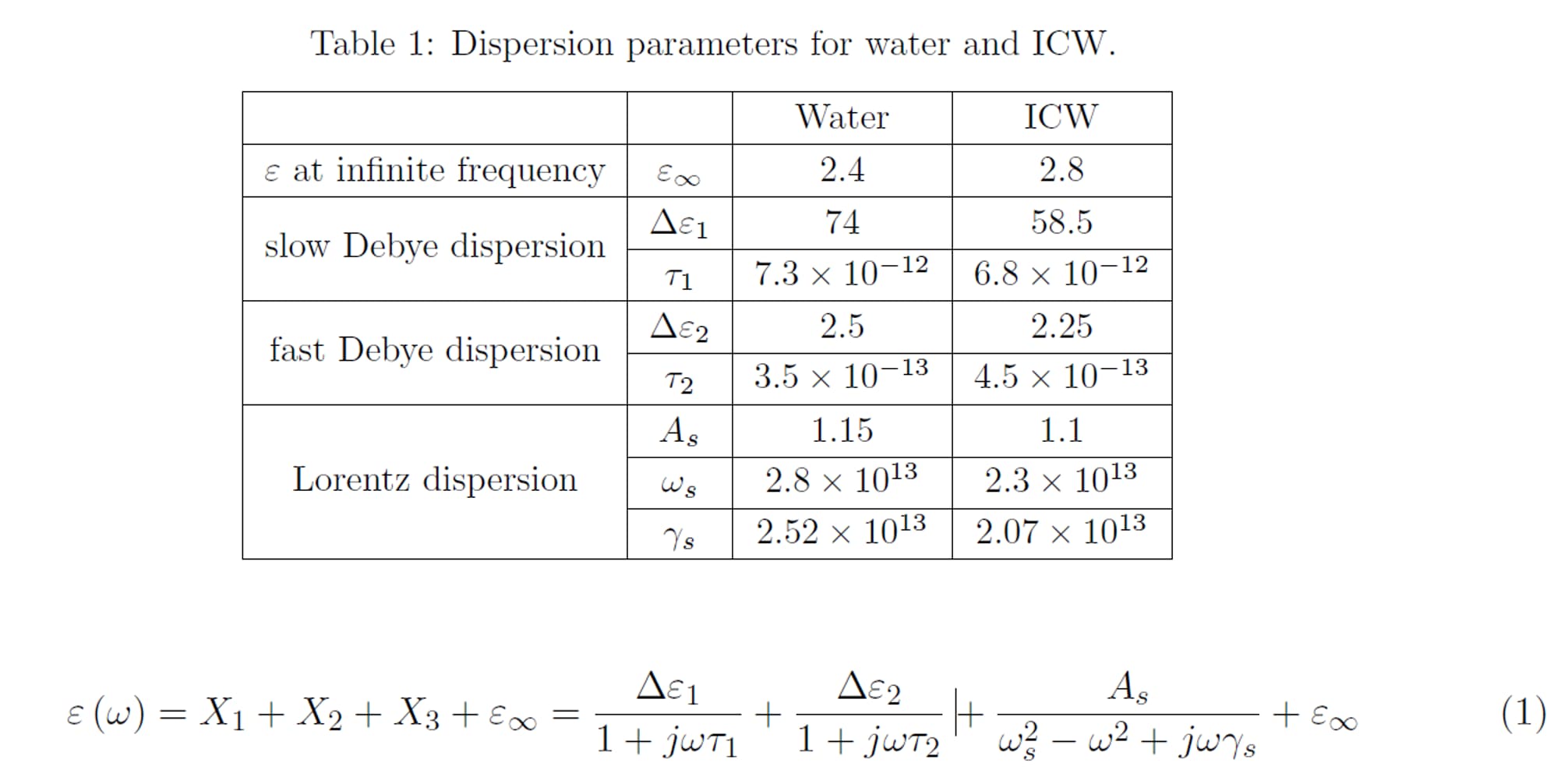
Parameters in (eq.1) are first calculated by fitting the equation to the dielectric properties measured with least squares assumptions. To improve the agreement between the properties obtained by (eq.1) and experimental value around 1THz, parameters are adjusted manually. Obtained values are shown in Table.1.

まとめ

シミュレーションで与えた物性を明示することは非常に重要です。マイクロ波領域の場合は一般的に複素誘電率を記載します。複素誘電率の虚部の記載はtanδで置き換えることも可能です。

複素誘電率は多くの物質で温度と周波数に対して依存性があります。このため固定物性値を使用した場合には想定した温度と周波数を記載するべきです。

周波数依存性を考慮した場合には使用した分散モデルを記載し、その中に含まれる分散パラメータを記載します。文例2の様に本文中に分散パラメータを記載するのが一般的ですが、分散パラメータが多い場合には文例3のようにtableを作成して示すことも一般的です。

妥当性の主張ー離散化とメッシュ、タイムステップ

文例

解析領域は150×150×20[mm]の矩形領域とし、1[mm]の厚さ形状を十分再現できるよう300×300×40セルのメッシュを生成し解析に用いた。またこのメッシュでCFL数が0.5となるようタイムステップΔtを設定した。

まとめ

一般的にメッシュに関しては解析領域と3次元方向のセル数または格子点数を示します。メッシュの妥当性は波長λを基準にメッシュ幅がλ / 10～20以下であり、解析領域内の形状を十分再現できる密度があることです。

解析に使用したメッシュは解析のモデル図と共に提示するのが望ましいです。特に再現すべき形状に対してどの程度の密度でメッシュが確保されているか直感的に理解できる図は重要です。

上記の例は等間隔メッシュの場合の例ですが、不等間隔メッシュやメッシュの一部分が細かいサブグリッド法などを用いた場合はそれらが理解されやすいように図と文章で説明することが重要です。

時間進行法であるFDTD法ではタイムステップも重要な情報です。タイムステップの値そのものを示すよりもCFL数を示す方が一般的です。

妥当性の主張ー境界条件

文例: キャビティ内部解析の例

導波管を導入したX方向負側の解析領域端部は12層のPMLからなる吸収境界条件とした。キャビティ内部壁に相当するその他の解析領域端部は完全導体壁を仮定し境界条件とした。

まとめ

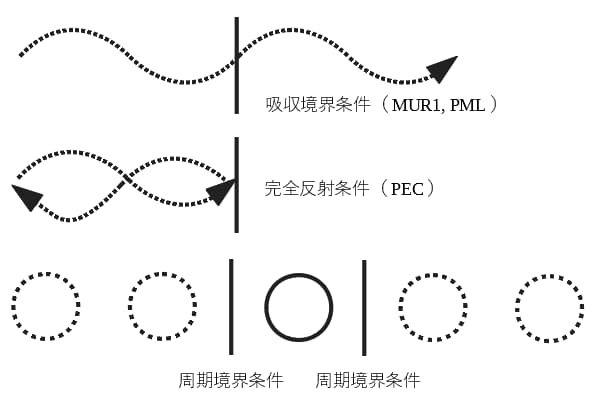
電磁波シミュレーションで用いられる境界条件は主に上に示した3種類です。MUR1及びPML(Perfect Matched Layer)は電磁波の反射を0にする条件として定式化されているため吸収境界条件と呼ばれますが実際には解放をモデル化する場合に使用されます。

完全反射反射条件PEC（Perfect Electric Conductor)は入射した電磁波を完全反射する条件です。導波管やキャビティ壁面はこの境界条件でしばしばモデル化されます。理想的な（導電率∞の）導体を仮定しているために、壁面での損失をシミュレートすることはできないので注意が必要です。

また周期的な構造を持つ電波吸収体のようなものをシミュレートする場合には周期境界条件を使用します。周期境界条件を用いると1周期の解析領域を計算するだけで、無限に同じ構造が続いていることを模擬できます。構造が距離を置いて存在する場合には、構造と解析領域境界の距離は構造同士の距離の半分になるように配置することに注意が必要です。

妥当性の主張ー収束性の確認

文例: ある点の電界強度の時系列データを示して収束性を示す

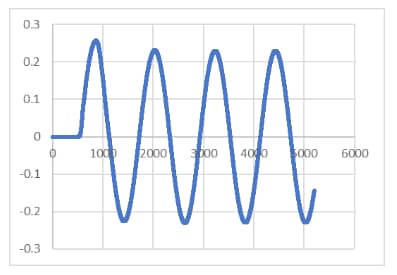
解析領域中心部における電界成分Eyの値が励振周期で一定の振幅で変化することを確認し約5000ステップで一定の電磁界に収束したことを確認した。

まとめ

FDTD解析は時間進行法であり求められる物理量は時々刻々変化します。このような状況で解析領域内に十分電磁波が行き渡り、系全体が周期的な変化をしていること、つまり収束性を確認するためには解析領域内の代表的な点で周期的に変化する値が得られていることを確認します。

収束（convergence）という言葉は一般的には反復計算法、例えば有限要素法（Finite Element Method）における逐次過緩和法（Successive Over Relaxation Method)などにおける残差が十分に小さくなることを指します。FDTDでも同じ言葉を使用していますが、物理的な意味はかなり異なりますので注意が必要です。

なおFDTD解析の場合、収束していない結果は「間違い」ではなく「過渡状態」を表します。パルスの解析などでは収束の概念そのものがないのでこの点は十分区別する必要があります。