4月の電磁波解析体験セミナーの開催（参加費無料）
4月26日に開催する電磁波解析体験セミナーについてお知らせいたします。 電磁波解析体験セミナーは毎月テーマを変えて開催しており、無料でご参加いただけ...
ブログ
電磁波解析
電磁波解析クラウドKeyFDTD on Cloudをリリースの...
弊社はこの度新サービスとして電磁波解析クラウドKeyFDTD on Cloudをリリースいたしました。 KeyFDTD on Cloudはクラウド上...
1月18日にテラヘルツ帯の電磁波解析体験セミナー開催
1月18日に開催する電磁波解析体験セミナーについてお知らせいたします。 電磁波解析体験セミナーは毎月テーマを変えて開催しており、無料でご参加いただけ...
2月15日に開催する電磁波解析体験セミナーについてお知らせいた...
電磁波解析体験セミナーは毎月テーマを変えて開催しており、無料でご参加いただけます。 本セミナーでは電磁波解析ソフトKeyFDTDを使用したシミュレー...
モルフォ蝶の構造色の解析
構造色はマイクロ～ナノスケールの微小構造によって特定の波長の光を散乱、反射することで生み出される色です。 同じ材質でも入射する角度や構造の一部が変化...
KeyFDTDで解析できる対象について
FDTD法は数百MHzの高周波から紫外～PHzまでの幅広い帯域を解析できます。 FDTD法は波長に近い構造物を得意とし、特に効率よく解析できます。 ...
ナノスケールの金属により進化する透明なフィルム
最近の電車の窓にブラインドが無いことにお気づきでしょうか。 これは電車の窓に紫外線に加えて、熱を感じる赤外線もカットするフィルムが利用されているため...
マイクロ波位相制御加熱のシミュレーションについて
マイクロ波加熱はレーダー用のマグネトロン開発中に発見された現象で、1940年台には電子レンジのように身近なところでも使われています。 火やヒーターな...
ナノ秒単位の高電界パルスの利用とシミュレーション
ナノ秒単位で高電界を加えるnsPEF（nanosecond Pulsed Electric Field）はガン治療への利用などが期待されています。 ...
KeyFDTDに追加されたSAR出力機能について
5月18日のアップデートでKeyFDTDにSAR(Specific Absorption Rate：比吸収率)の出力機能が追加されました。 SARは...
金属ナノ構造体のFDTD解析について
金属ナノ構造体はLSPR（局在表面プラズモン共鳴）による増強効果や合成技術の向上により、応用研究が活発に行われています。 FDTD法でLSPRをシミ...
KeyFDTD今後のアップデート予定
KeyFDTD今後のアップデート予定のお知らせです。 モデリングの標準オブジェクトに新たに「螺旋」を追加します。 螺旋はコイル、ばねなどを含むシミュ...
モスアイ構造
モスアイ構造は表面に付与したナノサイズの凹凸によって光の反射を抑えることを目的とした技術です。 液晶画面の表面にモスアイ構造を付与し、光の反射を低減...
電波吸収体のおはなし
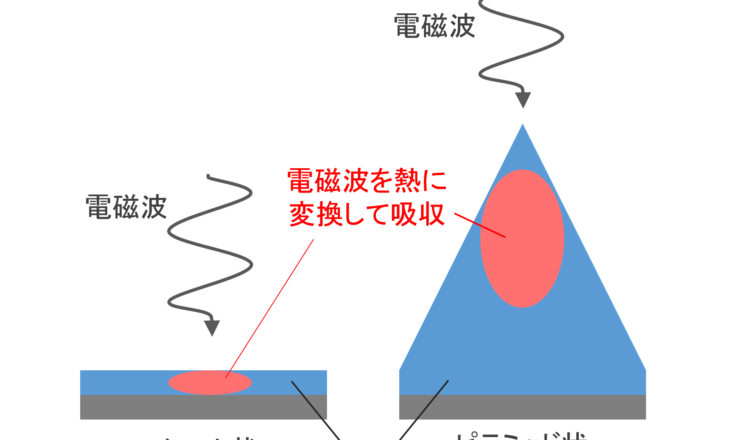
電波吸収体は電磁波を熱に変換して吸収するものです。 身近なところでは高速道路のETCの電波の吸収などに利用されています。 この電波吸収体で壁や天井全...
電子レンジは「危険」ではありません
WEBを見ていると、電子レンジは「危険なので対策グッズを購入しましょう」的なサイトが多くそのほとんどが詐欺に近い…。 結論から言うと電...
中空銀ナノ粒子の解析
電磁波解析ソフトKeyFDTDを使用して中空の銀ナノ粒子を解析しました。通常、銀は電磁波をほぼ反射しますが、ナノスケールでサイズ制御するとLSPR（...
Bull’sEye構造
Bull'sEye構造を通過するエネルギー強度と向き。 明日の「役に立つ電磁波解析セミナー」で、弊社 株式会社 科学技術研究所 科学技術部長...
KeyFDTDによる位相制御加熱シミュレーション例
株式会社 科学技術研究所 武藤拓人、三角哲平 第11回日本電磁波エネルギー応用学会、2017年11月10日 電磁波解析ソフトKeyFDTDを用いて1...
定在波(2)
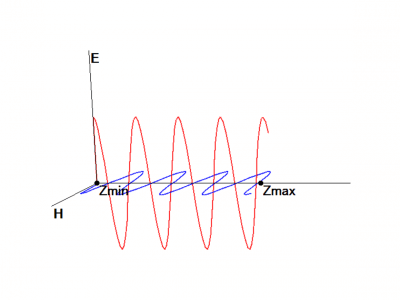
前回は電磁波の定在波を1次元電磁波解析ソフトKeyFDTDちゃんで可視化しました。 今回は定在波を式で表します。 まずは計算する物理の条件を設定しま...
定在波(1)
今回は電磁波の現象の１つ、定在波(Standing Wave)について記事にします。 定在波は、見かけ上は波が伝播せずにその場で振動しているかのよう...
1次元のFDTD法(6)
前回までに空間、時間についてマクスウェル方程式の離散化しました。 空間、時間の差分式は共に2次精度の式を導出しましたが、空間については精度を上げるこ...
1次元のFDTD法(5)
これまでにマクスウェル方程式を時間、空間について離散化しました。 今回は空間と時間の式を一つの式に合成します。 マクスウェル方程式のアンペールの式、...
1次元のFDTD法(4)
前回マクスウェル方程式を時間について離散化を行いました。 今回は、空間について離散化していきます。 まず、マクスウェル方程式を前回と同様に以下の形に...
レイリー散乱とミー散乱(3)
レイリー散乱とミー散乱は電磁波解析ソフトKeyFDTDの解析事例にもあります。 次の2枚の画像をご覧ください。 レイリー散乱 ミー散乱 これはレイリ...
1次元のFDTD法(3)
1次元FDTD第2回に紹介した離散化を使ってマクスウェル方程式を離散化していきます。 まず、マクスウェル方程式 $$nabla cdot bolds...
レイリー散乱とミー散乱(2)
今回はミー散乱を取り上げます。 ミー散乱は波長と同程度、または波長より大きい散乱体に電磁波を照射した現象のことです。 「晴れた日の雲が白いこと」がミ...
1次元のFDTD法(2)
FDTD法ではマクスウェル方程式を時間、空間で離散化して電磁界を計算します。 今回はその離散化について取り上げます。 離散化手法にはいくつか種類があ...
レイリー散乱とミー散乱(1)
今日は電磁波の重要な性質の一つ、散乱について取り上げます。 散乱は電磁波の進行方向に障害物（散乱体）があるとき、進行方向以外に電磁波が反れていく現象...
1次元のFDTD法(1)
FDTD法について KeyFDTDで使用しているFDTD法について1次元のFDTD解析を通して紹介します。 FDTD法は（Finite Differ...
電磁波を表す様々な単位
前回電磁波の呼び名に関する画像で横軸に波長を示しました。 波長とは、一定周期で振動する電磁波の一周期分の長さのことです。よくλで表され...