前回マクスウェル方程式を時間について離散化を行いました。
今回は、空間について離散化していきます。

まず、マクスウェル方程式を前回と同様に以下の形に変形します。

$$ frac {partial boldsymbol {E}} {partial t} = -frac {sigma} {varepsilon} boldsymbol{E} + frac {1} {varepsilon}(nabla times boldsymbol{H}) tag{1} $$

$$ frac {partial boldsymbol{H}} {partial t} = – frac {1} {mu} (nabla times boldsymbol{E}) tag{2} $$

この式において、( nabla times boldsymbol{H})、(nabla times boldsymbol{E})を各成分に分解すると、

$$
nabla times boldsymbol{E}
= left(
begin{array}{ccc}
frac{partial E_z}{partial y} – frac{partial E_y}{partial z} \[5pt]
frac{partial E_x}{partial z} – frac{partial E_z}{partial x} \[5pt]
frac{partial E_y}{partial x} – frac{partial E_x}{partial y}
end{array}
right)
tag{3} $$
$$
nabla times boldsymbol{H}
= left(
begin{array}{ccc}
frac{partial H_z}{partial y} – frac{partial H_y}{partial z} \[5pt]
frac{partial H_x}{partial z} -frac{partial H_z}{partial x} \[5pt]
frac{partial H_y}{partial x} – frac{partial H_x}{partial y}
end{array}
right)
tag{4} $$
今回はz方向のみの1次元FDTDを考えているため、( frac {partial} {partial z} )の項のみとなり、
$$
nabla times boldsymbol{E}
= left(
begin{array}{ccc}
frac{partial E_z}{partial y} – frac{partial E_y}{partial z} \[5pt]
frac{partial E_x}{partial z} – frac{partial E_z}{partial x} \[5pt]
frac{partial E_y}{partial x} – frac{partial E_x}{partial y}
end{array}
right)
= left(
begin{array}{ccc}
– frac{partial E_y}{partial z} \[5pt]
frac{partial E_x}{partial z}\[5pt]
0
end{array}
right)
tag{5} $$
$$
nabla times boldsymbol{H}
= left(
begin{array}{ccc}
frac{partial H_z}{partial y} – frac{partial H_y}{partial z} \[5pt]
frac{partial H_x}{partial z} -frac{partial H_z}{partial x} \[5pt]
frac{partial H_y}{partial x} – frac{partial H_x}{partial y}
end{array}
right)
= left(
begin{array}{ccc}
– frac{partial H_y}{partial z} \[5pt]
frac{partial H_x}{partial z} \[5pt]
0
end{array}
right)
tag{6} $$

電界と磁界はそれぞれ直交しているため、(E_x)、(H_y)と(E_y)、(H_x)の組み合わせになります。
(E_x)、(H_y)の組み合わせを取り上げると、(E_y=H_x=0)となるため、式（5）、（6）は、
$$
nabla times boldsymbol{E}
= left(
begin{array}{ccc}
frac{partial E_z}{partial y} – frac{partial E_y}{partial z} \[5pt]
frac{partial E_x}{partial z} – frac{partial E_z}{partial x} \[5pt]
frac{partial E_y}{partial x} – frac{partial E_x}{partial y}
end{array}
right)
= left(
begin{array}{ccc}
0 \[5pt]
frac{partial E_x}{partial z}\[5pt]
0
end{array}
right)
= frac{partial E_x}{partial z}
tag{7} $$
$$
nabla times boldsymbol{H}
= left(
begin{array}{ccc}
frac{partial H_z}{partial y} – frac{partial H_y}{partial z} \[5pt]
frac{partial H_x}{partial z} -frac{partial H_z}{partial x} \[5pt]
frac{partial H_y}{partial x} – frac{partial H_x}{partial y}
end{array}
right)
= left(
begin{array}{ccc}
– frac{partial H_y}{partial z} \[5pt]
0 \[5pt]
0
end{array}
right)
= – frac{partial H_y}{partial z}
tag{8} $$

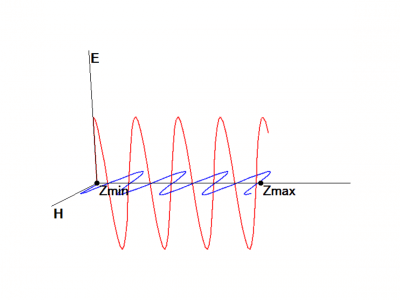
電磁界の空間配置は以下のようなYee格子をというものを用います。

この空間配置から電磁界の中心差分を取り、離散化すると式（9）、（10）のようになります。
$$
nabla times boldsymbol{E}
= frac{partial E_x}{partial z} approx frac {E_{x k Delta z} – E_{x (k-1) Delta z}} {k Delta z – (k-1) Delta z} = frac {E_{x k Delta z} – E_{x (k-1) Delta z}} {Delta z}
tag{9} $$
$$
nabla times boldsymbol{H}
= – frac{partial H_y}{partial z} approx frac {H_{y (k+1/2) Delta z} – H_{y (k-1/2) Delta z}} {(k+1/2) Delta z – (k-1/2) Delta z} = frac {H_{y (k+1/2) Delta z} – H_{y (k-1/2) Delta z}} {Delta z}
tag{10} $$

以上により空間について離散化ができました。次回に時間と空間の離散化を合成します。