フロー処理型マイクロ波加熱装置の電磁波ー温度連成解析（熱流体解析を用いないアプローチ）

1. 解析概要

本事例ではフロー処理型マイクロ波加熱装置について、電磁波解析と解析的手法を組み合わせ温度分布を求める例を示す。特定条件下では熱流体解析を用いない手法も有用であることを紹介する。

2. 解析条件

2.1 電磁波解析

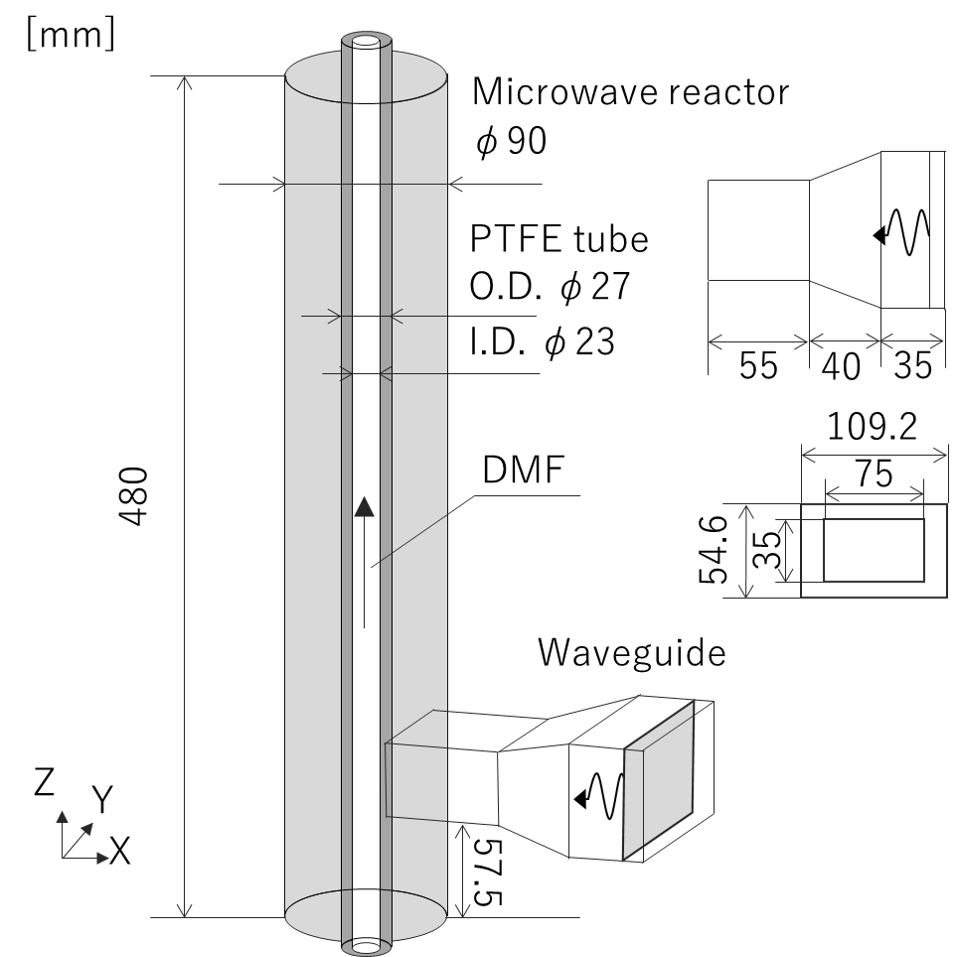
電磁波解析モデルはFig.1に示すように直径90[mm]の加熱炉に外径27[mm]、内径23[mm]のPTFEチューブを通し、一定の流速で下から上にN,N-ジメチルホルムアミド(DMF)が流れる系である。側面の矩形導波管から加熱炉に2.45[GHz]のマイクロ波を入力し、DMFを加熱する。使用した物性値をTable.1に示す。DMFは温度依存性を考慮した。

Fig.1 Simulation model

Table.1 Dielectric parameters

MaterialDielectric parameterThermal parameter

Vacuum	ε^* = 1.00+j0.00
PEC	σ = ∞
PTFE	ε^* = 2.10+j0.00	Heat transfer coefficient:2 [W/K m²] Emissivity:0.9 Temperature:293[K]
DMF	ε^* = 38.5+j5.66 (tanδ: 0.147) 293-303[K] ε^* = 37.4+j5.09 (tanδ: 0.136) 303-313[K] ε^* = 35.7+j4.50 (tanδ: 0.126) 313-323[K] ε^* = 33.7+j3.91 (tanδ: 0.116) 323-333[K] ε^* = 31.9+j3.32 (tanδ: 0.104) 333-343[K] ε^* = 30.7+j2.70 (tanδ: 0.0879) 343-353[K] ε^* = 30.3+j2.42 (tanδ: 0.0799) 353-[K]	Density: 944[kg/m³] Specific Heat: 2029[J/kg K] Temperature: 293[K] Inflow rate: 300[mL/min]

2.2 解析的手法による温度分布の導出

流路中のDMFについて径方向の加熱量、温度分布は一様と仮定した際の熱収支を(eq.1)に示す。流速は一定と仮定とすると、(eq.1)は位置に関する式(eq.2)に変形できる。

$\frac{\partial T}{\partial t} = \frac{1}{\rho C_p}(\kappa\Delta T-q_t(x)-q_r(x)+H_r(x)+q(x)) \cdots (eq.1)$

$\frac{\partial x}{\partial t} \frac{\partial T}{\partial x} = \frac{1}{\rho C_p}(-q_t(x)-q_r(x)+H_r(x)+q(x))$

$u \frac{\partial T}{\partial x} = \frac{1}{\rho C_p}(-q_t(x)-q_r(x)+H_r(x)+q(x))$

$\frac{\partial T}{\partial x} = \frac{1}{u \rho C_p}(-q_t(x)-q_r(x)+H_r(x)+q(x)) \cdots (eq.2)$

T:温度[K]、ρ:密度[kg/m³]、C_p:比熱[J/kg K]、κ:熱伝導率[W/K m²]、q_t:熱伝達により界面から移動する熱量[W]、q_r:放射熱[W]、H_r:反応熱[W]、q:加熱量[W]、u:流速[m/sec]

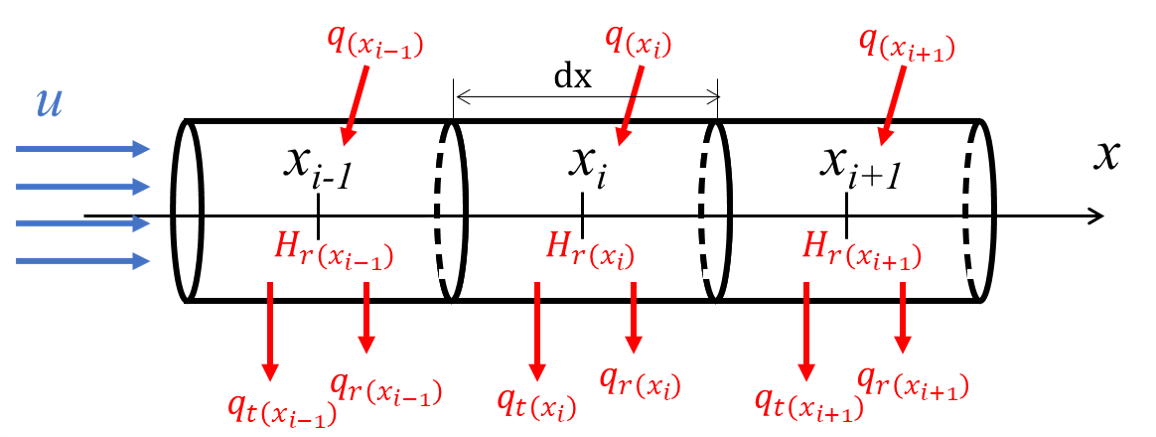
Fig.2のように流路を微小長さに分割、(eq.2)を離散化することで、Table.1の条件と加熱量分布から(eq.3)で各位置の温度を導出できる。

Fig.2 Discretization of the model

$\frac{\partial T}{\partial x} \simeq \frac{T(x_i)-T(x_{i-1})}{dx}= \frac{1}{u \rho C_p}(-q_t(x_{i-1})-q_r(x_{i-1})+H_r(x_{i-1})+q(x_{i-1}))$

$T(x_i) = T(x_{i-1})+\frac{dx}{u \rho C_p}(-q_t(x_{i-1})-q_r(x_{i-1}) +H_r(x_{i-1})+q(x_{i-1})) \cdots (eq.3)$

2.3 電磁波－温度連成解析

上記の電磁波解析と解析的手法による温度分布の導出を組み合わせて電磁波ー温度連成解析を行った。電磁波解析で得た各位置の加熱量を(eq.3)に代入し、DMFの温度分布を導出する。得られた温度分布に従って電磁波解析モデルに誘電物性を与え、再度電磁波解析を実施、温度分布が定常状態となるまで繰り返し行った。
初回のDMFには293[K]の物性値を全体に適用した。電磁波解析はTable.2の解析条件で、電磁波解析ソフトKeyFDTDを用いて行い、温度分布は表計算ソフトを用いて算出した。

Table.2 Analysis condition

Incident wave	Sine wave, TE₁₀ mode, 2.45[GHz]
Boundary condition	x,y:PEC, z:MUR1
Computational domain	200x120x520[mm]
Mesh size	1.94[mm]≒λ/63(in vacuum)
Timestep	3.24×10^-12[sec]
Input energy	1000[W]
Heating efficiency	90[%]

3. 解析結果

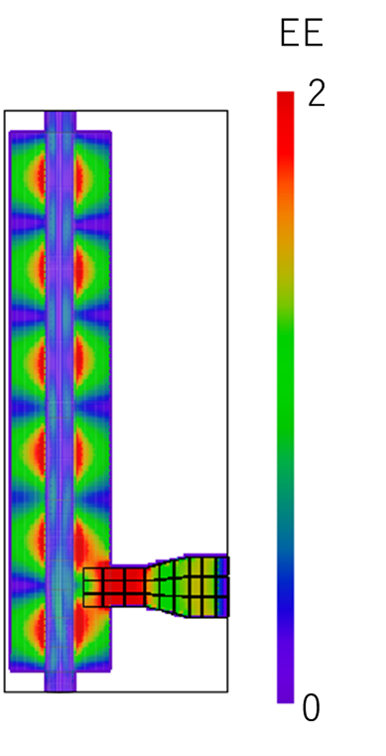
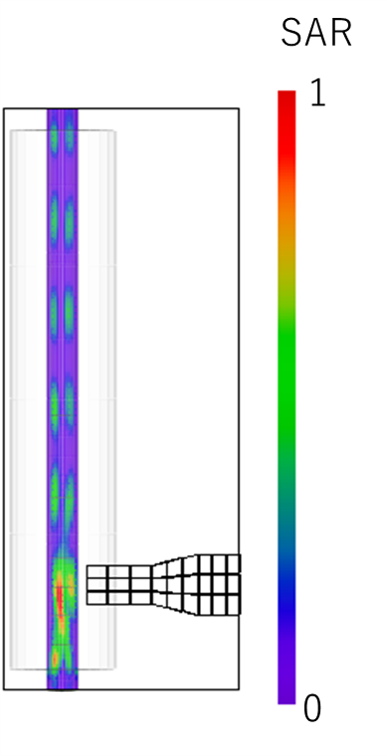
電磁波ー温度連成解析は5回目の解析で定常状態となった。定常状態の電界(EE)、加熱量(SAR)分布をFig.3に示す。加熱炉内に定在波が見られ、加熱量分布からDMFは直達波と定在波の両方で加熱されていると分かる。

(a)Electric field distribution

(b)SAR distribution

Fig.3 Simulation result

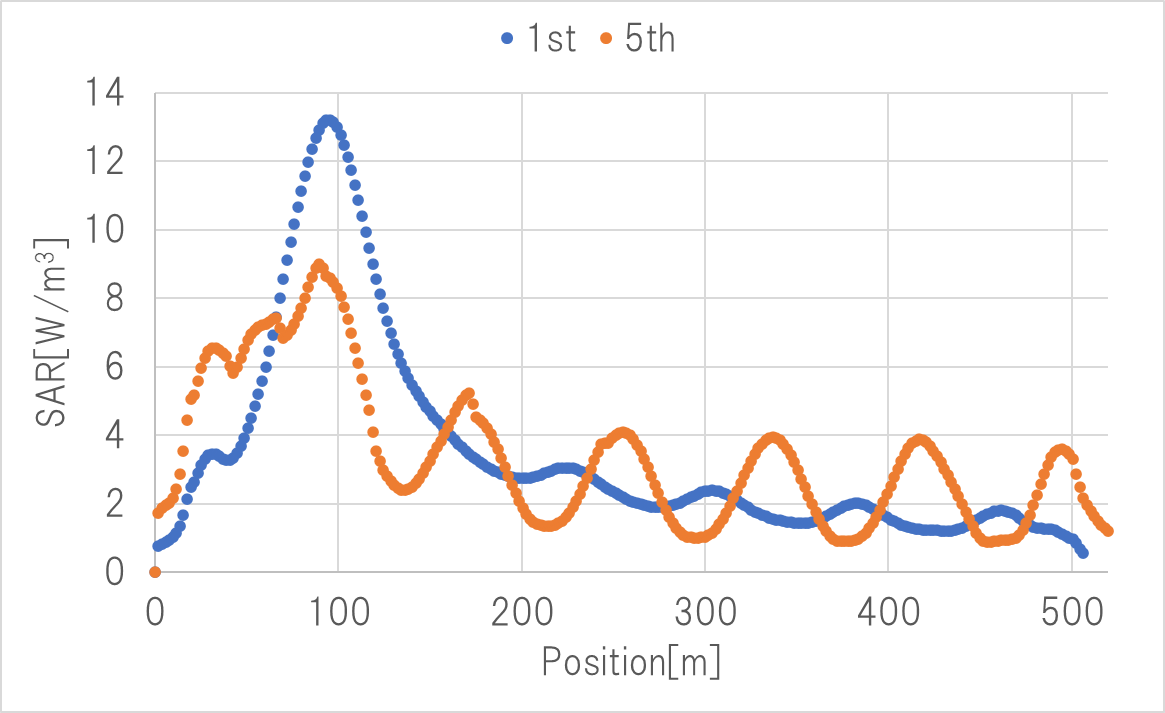
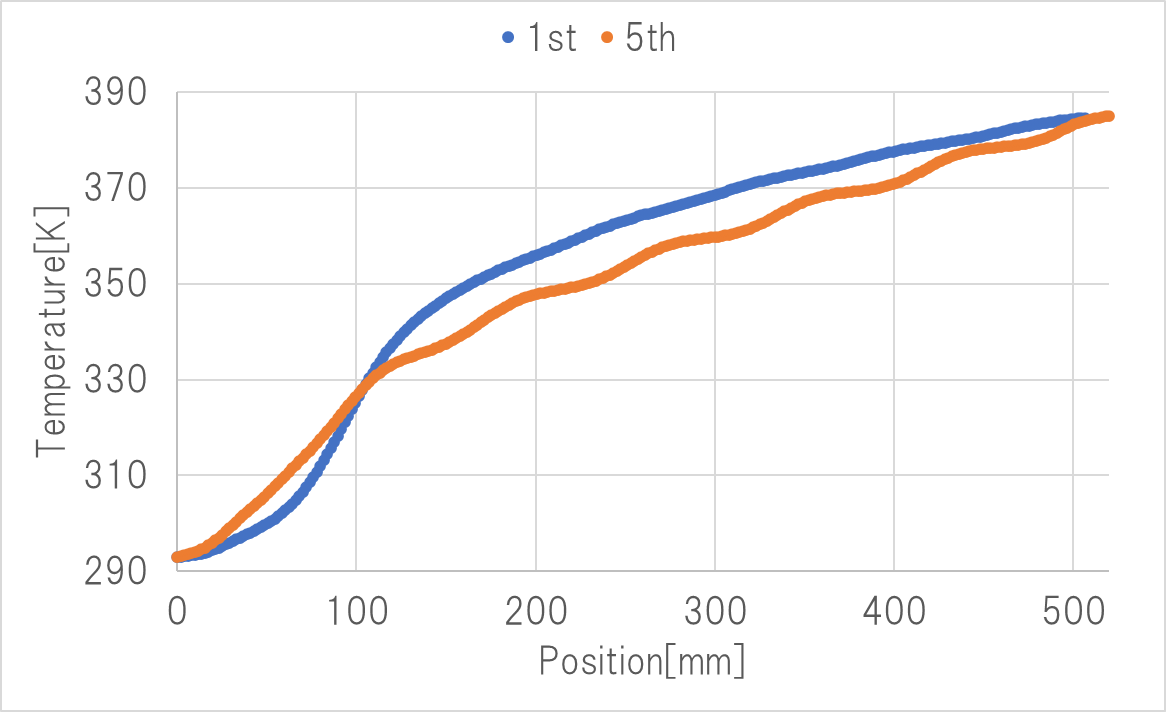
初回と定常状態におけるDMFの加熱量、温度分布をFig.4、Fig.5に示す。Fig.5の初回と定常状態の温度分布を比較すると最大±10[K]程度差が生じている。
Fig.4から温度差の原因は加熱様式の違いと考えられる。DMFは温度が低いほどtanδが大きく、加熱されやすい。そのため温度依存性を考慮しない場合は、直達波による加熱が支配的となる。一方温度依存性を考慮すると、直達波が当たる位置より手前でDMFが昇温するため、直達波の加熱量が減少、その分定在波の加熱量が増大する。
以上から、今回取り上げた流通系の加熱はFig5のように緩やかに昇温する系である。

Fig.4 SAR distribution

Fig.5 Temperature distribution

4. まとめ

電磁波解析ソフトKeyFDTDと解析的手法による温度分布導出を組み合わせて電磁波-温度連成解析を行った。熱流体解析を用いずとも、流通系のマイクロ波加熱について物性値の温度依存性を考慮した加熱量、温度分布を得られることを示した。

あとがき

CAEを扱うにあたって複数の解析手法を選択肢に持つことはプラスです。
本事例はそれを示す好例の一つでした。
弊社科学技術研究所では電磁波解析、熱流体解析、構造解析といった様々なCAE技術を基盤に技術コンサルタント、受託解析、受託開発をいたします。複雑に思われるシミュレーション課題につきましても是非お問い合わせをお待ちしております。

お問い合わせ・資料ダウンロード・入門動画視聴のお申し込みはこちら
お問合せフォームを開く