FDTD法による電磁波解析

Electromagnetic Wave Analysis Using the FDTD Method

FDTD法とは/What is the FDTD Method?

FDTD法とは、以下の(1)式で表されるMaxwell方程式を時間的(Time)、空間的(Domain)に離散化し陽的な時間進行法を用いて経時的な電磁界強度を求める手法です。

ここで、電界： $E\,\mathrm{[V/m]}$ 、磁界： $H\,\mathrm{[A/m]}$ 、電束密度： $D\,\mathrm{[C/m^2]}$ 、磁束密度： $B\,\mathrm{[T]}$ 、電流密度： $I\,\mathrm{[A/m^2]}$ です。

The FDTD method (Finite-Difference Time-Domain method) is a technique for determining the time-dependent electromagnetic field intensity. It discretizes Maxwell’s equations, represented by Equation (1) below, in both the time (Time) and spatial (Domain) domains and employs an explicit time-marching scheme.
Here, we define an electric field as $E\,\mathrm{[V/m]}$ , a magnetic field as $H\,\mathrm{[A/m]}$ , an electric flux density $D\,\mathrm{[C/m^2]}$ , a magnetic flux density $B\,\mathrm{[T]}$ , and a current density $I\,\mathrm{[A/m^2]}$ (A current density is often indicated by $J$ , but in this site, it is indicated by $I$ to avoid confusion with the imaginary unit $j$ ).
(FDTD method is an abbreviation for Finite-Difference Time-Domain method)

(1) $\begin{eqnarray*} \nabla \times \bm{E}(t, \bm{x}) + \frac{\partial \bm{B}(t, \bm{x})}{\partial t} &=& 0 \\ \nabla \times \bm{H}(t, \bm{x}) - \frac{\partial \bm{D}(t, \bm{x})}{\partial t} &=& \bm{I}(t, \bm{x}) \end{eqnarray*}$

これから、FDTD法について具体的に分かりやすく説明します。

なお、電流密度は $J$ で示すケースも多いですが、本ページでは虚数単位 $j$ と混同しないように $I$ で示します。

*FDTD法とは、Finite-Difference Time-Domain methodの略号です。
Keyword:FDTD,FDTD法,電界,磁界,電束密度,磁束密度,Maxwell方程式,FDTD method,Finite-Difference,Time-Domain method,electromagnetic field,Maxwell equation

格子は多くの場合、図1のような電界及び磁界ベクトルの配置が半格子ずれたスタガード格子(Staggered Grid)を用います。FDTD法では電磁波の波形を再現するために格子は解析対象とする波長よりも十分に小さい必要があります。かつ時間的な陽的解法ですので、時間進行法に用いるタイムステップは格子幅 $\Delta h$ 及び光速 $c$ を用いてCFL条件(Courant-Friedrichs-Lewy Condition; クーラン条件)から求められる $\dfrac{\Delta h}{c}$ が上限値となります。従って、電磁波の伝搬の様子を空間・時間的に可視化できるという大きなメリットがあり、また解析領域の大きさと解析対象波長が近い場合には非常に効率的に解が得られます。一方で解析領域が波長の100倍程度になると格子点数が膨大なものとなり解析が困難になるというデメリットがあります。

In most cases, a staggered grid is used, where the arrangement of the electric and magnetic field vectors is offset, as shown in Figure 1. In the finite-difference time-domain (FDTD) method, the grid must be sufficiently smaller than the wavelength of the electromagnetic waves being analyzed to accurately reproduce their waveform. Additionally, since the method employs an explicit time-stepping scheme, the time step used for time evolution is constrained by the Courant-Friedrichs-Lewy (CFL) condition (Courant condition), which sets an upper limit of $\dfrac{\Delta h}{c}$ .
As a result, a significant advantage of the FDTD method is its ability to spatially and temporally visualize electromagnetic wave propagation. Moreover, it is highly efficient when the size of the analysis domain is comparable to the wavelength being analyzed. However, a major drawback is that when the analysis domain becomes approximately 100 times the wavelength, the number of grid points becomes enormous, making the computation challenging.

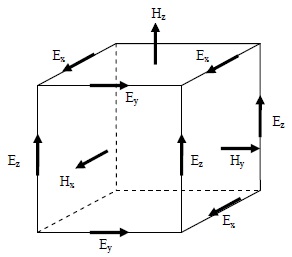
図1 スタガード格子

可視光(波長400nm～800nm程度)を扱う場合にはサブマイクロ～マイクロメートルの解析領域を対象とするような問題で非常に効率的な解析が可能です。特にナノスケールの構造をもった物体の電磁波の反射・散乱・透過特性の解析やプラズモン解析などでは多くの実績があります。また電子レンジのようなマイクロ波加熱問題も波長と解析領域の大きさが近い場合が多く効率よく解析ができます。さらに波長の長い電波は建物の壁面を考慮することはできませんが、建物を一つの物体と見立てれば大空間における解析も可能です。

When dealing with visible light (wavelengths of approximately 400 nm to 800 nm), highly efficient analysis is possible for problems that target submicron to micrometer-scale analysis domains. In particular, there is extensive experience in analyzing the reflection, scattering, and transmission properties of electromagnetic waves in objects with nanoscale structures, as well as in plasmon analysis. Additionally, microwave heating problems, such as those involving microwave ovens, can also be analyzed efficiently since the wavelength and analysis domain sizes are often similar. Furthermore, while long-wavelength radio waves cannot account for building walls, it is possible to analyze large spaces by treating buildings as single objects.

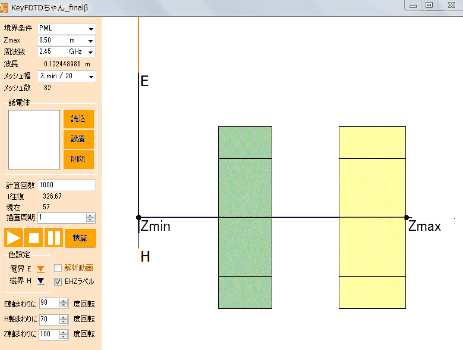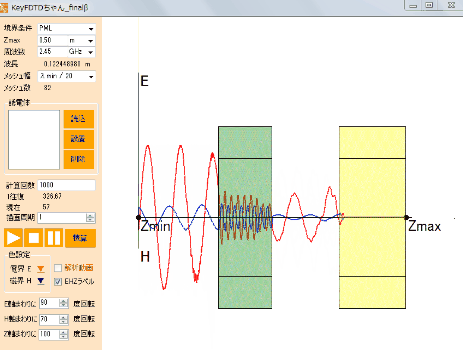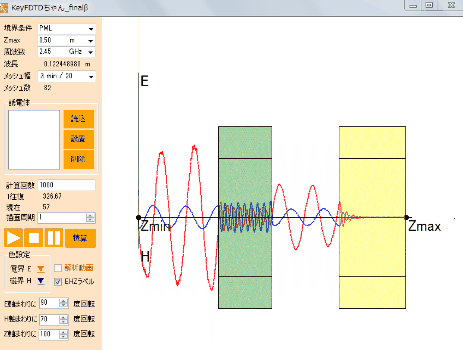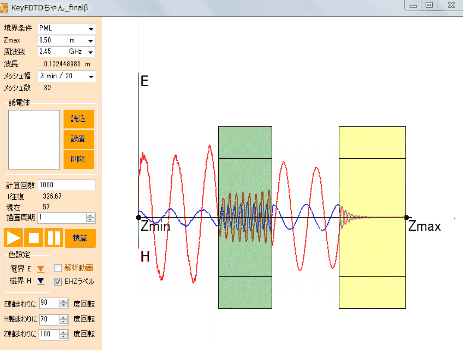
図2 電磁界の可視化様子（赤:電界、青:磁界）
（フリーソフト「KeyFDTDちゃん」の計算サンプル）
KeyFDTDちゃんは無料でお使いいただけます。

Figure 2: Visualization of the Electromagnetic Field (Red: Electric Field, Blue: Magnetic Field)
(Calculation Sample from the Free Software “KeyFDTD-chan”)
KeyFDTD-chan is available for free.

お問い合わせ・資料ダウンロード・入門動画視聴のお申し込みはこちら
お問合せフォームを開く

FDTD法とは

FDTD法による電磁波解析