【電磁波解析を用いた研究計画】

結果までの難所　解析時間

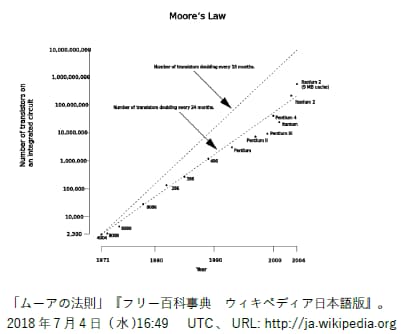
電磁波シミュレーションは非常に計算量が多く、コンピュータの性能を駆使した技術です。コンピュータの処理速度は2年で2倍になるというMooreの法則として知られ、急速に高度化しています。

一方で現在でも解析時間は常に問題です。シミュレーションの計算量が解析空間の「体積」に依存するためです。解析速度が2倍になっても各辺1[m]の立方体が1.26[m]の立方体になる程度にしか拡大できません。

解析時間を短縮する最も根本的で重要な事はメッシュの削減です。メッシュ数の減少はメッシュ幅の増加を伴い収束までの解析ステップ数を減少させる効果もあります。3次元解析の場合各方向のメッシュ数を80%減じると解析時間は40%程度短縮されます。

またメッシュ幅の増大は解析の安定性にも寄与します。空間解像度が低下するため精度の低下は避けられませんが、実用的な精度と計算時間の短縮のバランスをとることが大事です。

解析モデルのメッシュ数を減らす場合の注意点は薄板や容器の壁面などが再現できなくなる場合がある点です。この場合には解析結果に大きく影響しない範囲で、薄板や容器の壁面の厚みを厚くして、減じたメッシュでも形状が再現できるように調整します。

結果までの難所　物性値

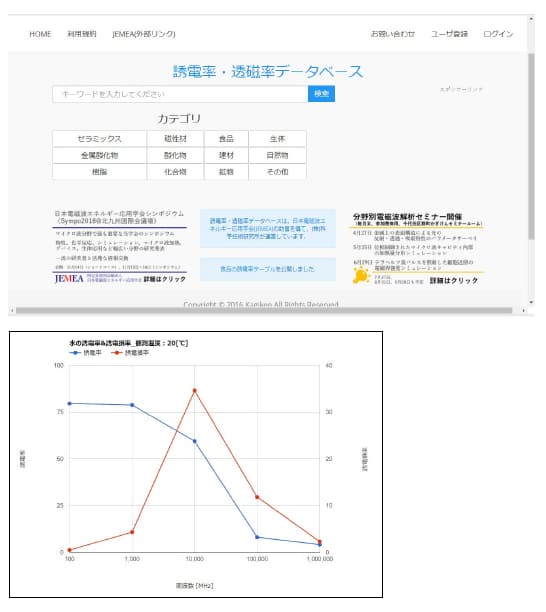
電磁波シミュレーションを行う場合には、想定する波長・温度における物性値の取得が必要です。最低限誘電率と透磁率の値が必要ですが、扱っている物そのもののこれらの値を見つけるのは意外と難しいものです。

誘電率・透磁率データベースでは2000物質60000件以上のデータを保持していますが、データが見つからないことも少なからずあります。究極的には測定が必要ですが、研究の本題から外れる場合は類似物質からの類推も一般的な選択肢です。なお透磁率は磁性を持たない物質の場合ほぼ1で間違いありませんが、磁性体、反磁性体の場合にその値を知るのが難しいのは誘電率の事情とそう違いありません。

結果までの難所　低い収束性

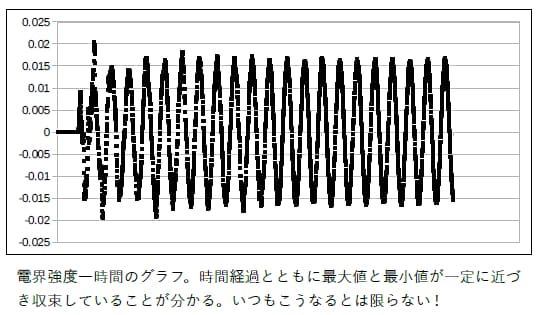
FDTD法による電磁波解析でいう「収束性」はFEMなどで言われる反復解法における残差が十分に小さくなることを持って判断する収束とはやや異なります。FDTD法は時間進行法なので各計算ステップにおける電磁界分布は常に正しいと言えます。

一方で実験などで測定される電磁界はマイクロ秒単位で変化する電磁界ではなく実用的な時間（例えば1秒とか）スケールを持ちます。この時間スケールでは電磁波は対象の領域に十分行き渡って、各位置で定在波が観測されます。

FDTD法は電磁界がない状態に電磁波を入射し、電磁波の伝搬をシミュレートし、最終的に定在波の分布を得ます。解析領域や解析対象によっては実質の伝搬成分が見えなくなってすべての位置で定在波が観測される状態になるまでに時間がかかる場合があり、このようなケースを収束性が悪いと呼んで極力避けるようプランを調整します。

物理現象として収束が遅い場合には、メッシュを減らすなどして同じ計算時間でも解析ステップを多く実行できるようにするのが一般的です。また薄い・細い・鋭い形状を含む解析は一般に収束性が悪くなります。この場合は解析の主旨に反しない範囲で形状を少し、厚く・太く・鈍くすることで収束性が改善できます。

結果までの難所　発散

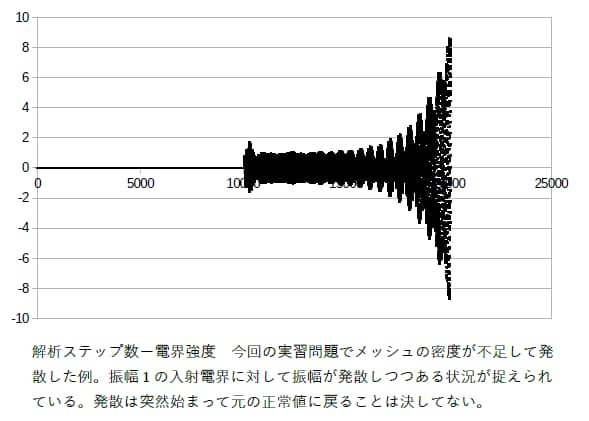
FDTD法は比較的安定した計算手法ですが様々な原因で解析が物理的な意味を失う「発散」が発生します。主な原因は、メッシュ密度の不足、不適切な境界条件の設定の2つです。

前者については解析領域内部の最短波長λとしてメッシュ幅がλ/10を超える場合に発生することがあります。この時のλは誘電率及び透磁率を考慮した波長短縮後の値を用いる必要があります。自由空間の伝搬波長を用いてメッシュ密度が不足する設定をしてしまわないことに注意が必要です。

後者は物体と物体の隙間にメッシュが1メッシュしか含まれない場合などに発生しやすく、この傾向は物体が金属（PEC）の場合に顕著になります。また解析領域の端部近傍に配置された励振源なども発散の原因となります。